991117數位學習研究方法

圖一

中央極限定律

•  中央極限定律（The Central Limit Theorem）是一個非常有用的定律，因為它描述了平均數之樣本分配的特質。這個定律如下：

•  當母群存在著變異數和平均數時，如果樣本的樣本數夠大，則樣本平均數形成的機率分配（稱為平均數的樣本機率分配；sampling distribution of means）會趨近於常態分配；且當樣本數增大時，樣本機率分配會越趨近於常態分配。

•  http://youngthinker.asia/resources/download-slide.php?slide_id=486

樣本平均數─

• 假定我們自母群中，一個接著一個去抽樣本人數(sample size)為N的多個樣本，每抽取一樣本便得到一個平均數，在N足夠大的時候，例如N=30以上或N=50以上，這些平均數的次數分配也會非常接近常態分配。

• 每一次抽出來會在母群平均數的附近，具有一定的代表性，但不完全可以代表母群平均數。最好的的情況是樣本平均數，就是母群平均數。抽很多次樣本的時候，母群平均數會剛好會在每一個樣本平均數的範圍內。

• 範圍愈小準確度低。

• 範圍愈大準確度高。

例一:平均數5.5假設你有一次抽出的樣本，平均數是6。

每次抽4~8之間，合理的推斷機率。

假如抽3~9之間，準確度99%

4~8之間準確度95%。

5~7之間準確度80%。

如果你想知道母群平均數在哪?從樣本平均數去擴大，就找的到母群平均數。

區間估計(Interval Estimation)

•    未知母體參數的區間估計式是一個公式，告訴我們如何利用樣本觀察值計算一個區間的上界與下界，稱為信賴界限，使得在重複抽取樣本時，未知參數落在計算的信賴界限的比例達到需要的準確度，稱為信賴水準。

•    信賴界限的值隨樣本而變，是一組隨機變數，因此形成的區間是隨機區間。前提是如果我們有取樣多次的機會，可能就會很準確。

•    http://www.mcu.edu.tw/department/management/stat/ch.../chap10.pdf

平均數的考驗

圖二

抽出5.7、5、6.3、4.7、5.4、4.8、6.7、5.3、7.1、5.4、4.2、6.1。

1~10平均分數5.5

今天如果一個樣本平均數是7，如果我抽出是8.2一定不是從這裡抽的，但抽到7.6有可能的。

圖三

有一個班級，全班智商加起來是130。

兩個班級，A班智商100，B班智商120。

抽到105>A是抽樣誤差。

抽188>B是抽樣誤差。

抽111>是A或B？

平均數+誤差=結果

100+E=111

E=11

兩類錯誤

α (第一類型錯誤)：原來是α ，說他非α 。

β (第二類型錯誤)：原來是β ，說他非β 。

第一類~我要幫小孩找媽媽。

第二類~有兩小孩，我要看媽媽是不是同一個人?

第三類~三小孩，我要找是不是同媽媽?(ANOVA單因子變異數)

前測是一個抽樣，後測也是一個抽樣

如果開學後

A和B考了兩次統計，A和B的分數都一樣。代表是同一個母群。

A和B考了兩次統計，A和B的分數不一樣。代表是不同一個母群。

態度量表

做一個40人次，分三組，態度量表，量表分數有1~5。一共有十個題目，量表最低分是1分，最高分是5分。B~K是題目。上面是題目，左邊是人數(流水號)。

EXCEL，變成整數，最少是1最高是5

SPSS中分三組，假設是甲、乙、丙三個班的

EXCEL語法(整數及隨機出現1~5數字)

=INT(1+RAND()*5)

=INT(RAND()*5)+1

圖四

最左排是組別，分三組，每組四十人，所以寫1寫40次，接著2寫40次，3寫40次，依此類推。

圖五

下圖~分析>比較平均數法>單因子變異數分析

圖六

下圖~因子放組別，題目放依變數清單。

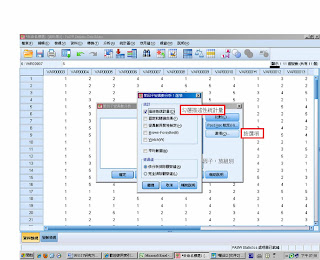
圖七

下圖~按選項>勾選描述性統計量

圖八

下圖~把平均數全部加起來，平均數會等於3。

圖九

自由度要N-1，

組間

因為分3組，所以自由度是2。整個加起來120，自由度減1，所以是119。

圖十

顯著性差異(significance level)，是一個統計學名詞。它是統計學（Statistics）上對數據差異性的評價。當數據之間具有了顯著性差異，就說明參與比對的數據不是來自於同一總體（Population），而是來自於具有差異的兩個不同總體，這種差異可能因參與比對的數據是來自不同實驗對象的。

顯著性差異是一種有量度的或然性評價。比如，我們說A、B兩數據在.05水平上具備顯著性差異，這是說兩組數據具備顯著性差異的可能性為95％。兩個數據所代表的樣本還有5％的可能性是沒有差異的。這5％的差異是由於隨機誤差造成的。

實驗結果達到.05水平或.01水平，才可以說數據之間具備了顯著性差異。在作結論時，應確實描述方向性（例如顯著大於或顯著小於）。

http://zh.wikipedia.org/zh-hant/%E6%98%BE%E8%91%97%E6%80%A7%E5%B7%AE%E5%BC%82
顯著性:發生機率多大。
希望正確率是99.5%，所以就是0.05的誤差。

希望正確率是99%，所以所以就是 0.01的誤差。

理論上我們這次做的不應該有顯著性

顯著性~推論發生錯誤的機率。推論又叫假設(hypothesis)，發生錯誤的機率是小於0.05(有顯著)。所以是對的。

如果大於.05，就代表他們發現錯誤的機率是一樣的，你就不能說他們是不一樣的(沒有顯著)。

95%  p<0.05*

99%  p<0.01**

99.9% p <0.001***

F檢驗

虛無假設是三組都一樣。

我們的顯著性是看α。

SPSS用獨立樣本T檢定

分析>比較平均數法>獨立樣本T檢定

圖十一

因為有三組，但每一次都比較兩組，所以只能勾選1和2 / 2和3 / 1和3 比較。

按定義組別>所以只能打 1和2 / 2和3 / 1和3 比較。數字就是組別。(一次只能比較兩組)

圖十二

按繼續

圖十三

F檢定如果有顯著，假設變異數是相等。

寫論文的話，看自由度和顯著性(雙尾)。

T檢定上下兩排不一樣，就看下面的那行。

顯著性(雙尾)

圖十四

顯著性(單尾)

圖十五

1.改變第三組資料。

2.用ANOVA找出有顯著性(<0.05)。

3.用T檢定找出第二組和第三組差別。(最有顯著和最沒顯著的)比較1.3或2.3資料。

4. 比較T檢定報表之不同。

資料來源

林清山(民66)。第十章推論統計的基本概念。載於張春興、楊國樞、文崇一(主編)，心理與教育統計學(185頁)。台北市：台灣東華。

胡志偉(民99年11月23日)。心理與教育統計學。取自http://youngthinker.asia/resources/download-slide.php?slide_id=486

民99年11月23日取自http://www.mcu.edu.tw/department/management/stat/ch.../chap10.pdf
維基百科(民99年11月23日)。顯著性差異。取自http://zh.wikipedia.org/zh-hant/%E6%98%BE%E8%91%97%E6%80%A7%E5%B7%AE%E5%BC%82